Räkna med bråk

Vad är då bråk?

Bråk beskriver delar av någon slags helhet eller delar från ett antal föremål. Här är det väldigt viktigt att vi då uppmärksammar att det handlar om delning i exakt lika stora delar.

Bråk används för att uttrycka andelar av en kvantitet eller mängd. Förr använde vi tal i bråkform i högre utsträckning i vårt vardagsliv än vad vi gör idag. Skolverket lyfter några intressanta exempel: förr mätte och uttryckte man avstånd som fjärdingsvägar (fjärdedelar av en mil). I affären användes ett kvarts kilo och en halv liter när man handlade. I recept var mått angett som 1⁄4 kg, 1⁄2 liter etc. Idag uttrycks storheter ofta i decimalform: (1,5 m), 3 kilo och 400 gram (3,4 kg) och så vidare. Men det är fortfarande lika viktigt att förstå och kunna uttrycka storleken av olika andelar. Bråkform är också grundläggande för att sedan kunna förstå decimalform och procent.

Att utveckla förståelse när det gäller bråk är en process där kunskapen gradvis breddas och fördjupas. Bråk kräver en hög abstraktionsförmåga.

Fyra grundläggande aspekt av bråk

1. Alla delar måste vara lika stora för att de ska vara bråkdelar.
2. Nämnaren visar i hur många delar en hel har delats.
3. Ju större nämnaren är, jämfört mot täljaren, desto mindre är bråket eftersom varje del blir mindre.
4. Täljaren visar hur många delar av helheten vi har.

Varför är bråk svårt?

Enligt Nationellt Centrum för Matematikutbildning (NCM) är det svårt att förstå bråk för att det finns så många sätt att tolka och skriva tal – t.ex. är alla dessa lika stora: 1,25, 125%, 5/4 och 1 1/4. Det vanligast problemet barn har i början är att man inte uppfattar att delarna i bråk måste vara lika stora. Samtidigt så brukar det fungera ganska bra så länge man håller sig till halvor och fjärdedelar eftersom det då handlar det om upprepad halvering. Även åttondelar hör hit. Problemen brukar uppstå när man kommer till tredjedelar. Ett exempel kan vara att man ska dela ett äpple på tre, delar det på hälften och sedan delar den ena halvan så att det blir tre delar. Resultatet blir ju ett halvt äpple och två fjärdedels äpple och inte tre tredjedelar. Likadelningsprincipen måste grundläggas tidigt. 

Det förekommer ofta missuppfattningar om storleken hos tal i bråkform. Den ena är att en stor nämnare betyder att det är ett större tal och den andra att 9 i nämnaren betyder att talet är nästan en hel. 

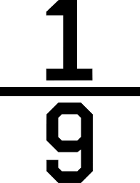
Barn vet att 9 är större än 3 och därför kan de lätt tänka att en niondel är stor och en tredjedel är liten. Det stämmer ju inte riktigt – 1/3 är ju större än 1/9. Jämför i cirklarna nedan:

Jämföra bråk

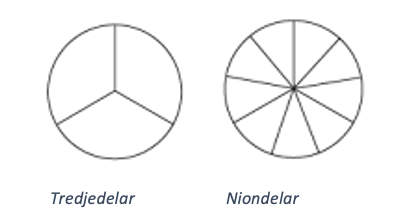
För att kunna jämföra bråk behöver barnen förstå att bråkdelarna är lika stora delar av mängd eller tal.

Ett bråkplank är också väldigt bra att använda för att jämföra och göra bråkstorleken tydlig. Ett sådant kan du rita upp hemma genom att vika, eller rita direkt ett papper och färglägga som nedan.

Öva på bråk tillsammans hemma

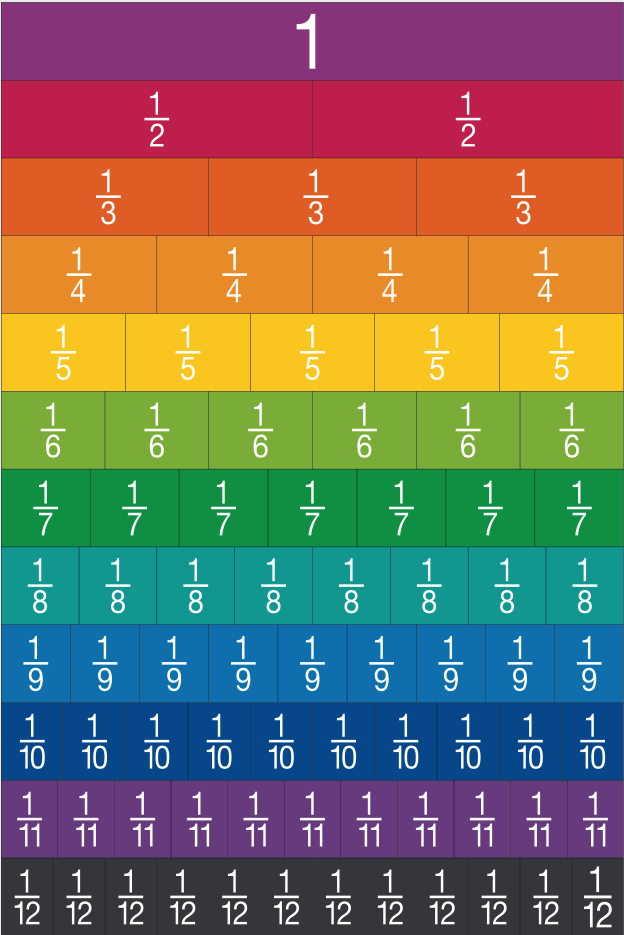
Det finns massor med olika sätt att prata om bråk hemma för att göra det lättare att fatta för barn. Till exempel kan ni prata om hur ni delar pizzan/chokladkakan i två lika stora delar blir det två halvor. Delar ni sen upp i fyra lika stora delar då blir det fjärdedelar. Varför inte prova att dela i åttondelar? Om ni sedan äter upp ½ så har ni en ½ eller 2/4, 4/8 kvar. På detta enkla sätt kan du introducera bråkräkning för ditt barn.