När man avancerar inom division och börjar hantera större siffror blir det nödvändigt att använda sig av division med uppställning. Då är det viktigt att ha bra kontroll på de grundläggande reglarna inom multiplikation och även förhållandet mellan multiplikation och division.
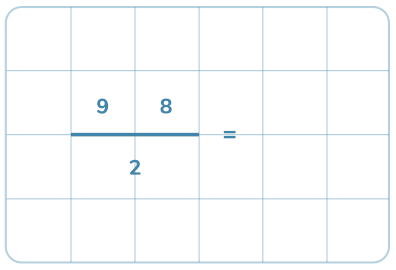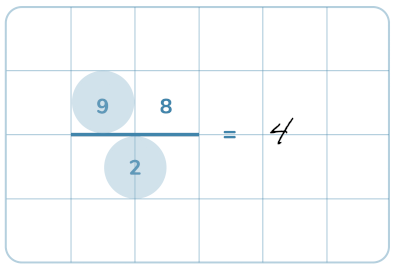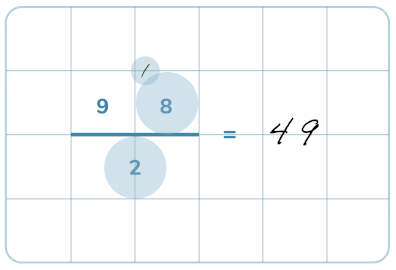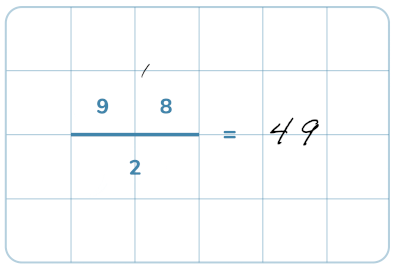
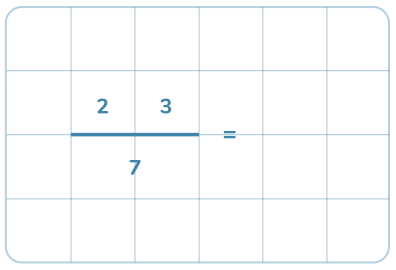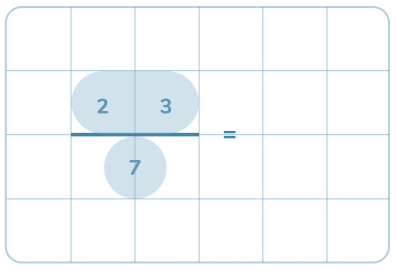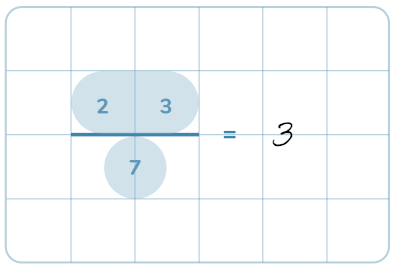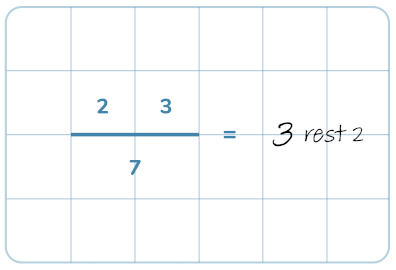
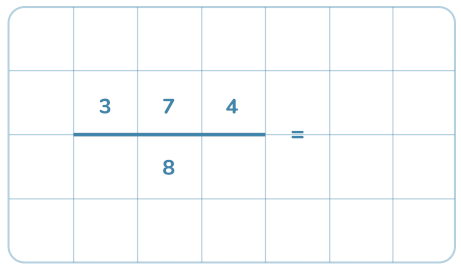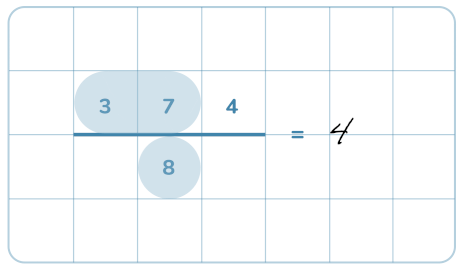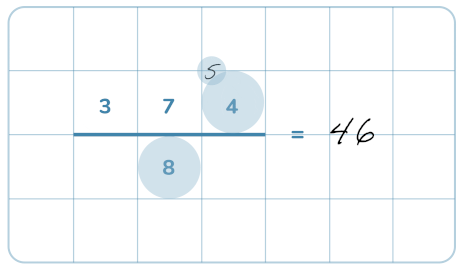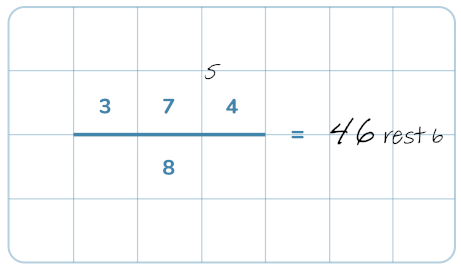
Här repeterar vi de grundläggande kunskaparna som behövs för division och även visar hur man gör för att dividera med uppställning.
Division är ett av de fyra räknesätten och introduceras efter multiplikation. Division kan ses som omvänd multiplikation och multiplikation som omvänd division, de är varandras inversa operationer, ex 12/4=3, 3*4=12. Men det finns även viktiga skillnader mellan de två räknesätten – så som den kommutativa lagen som säger att vi kan välja i vilken ordning vi multiplicerar 3*4 = 4*3, resultatet blir det samma, nämligen 12. Denna lag gäller för multiplikation, men inte för division – 12/4 är inte samma som 4/12!
Om ett barn kan sina multiplikationstabeller blir det en fördel i mötet med division, eftersom det då blir lättare att behärska divisionstabellen. Det blir även lättare att få dem upptäcka sambanden mellan de olika räknesätten.
Division brukar man starta med i 8-9 års åldern. Det finns två olika divisionstankar och dessa är innehållsdivision och delningsdivision. Innehållsdivision kan ses som upprepad subtraktion och delningsdivision som likadelning.
Divisionsuppställningar kan man göra på olika sätt men det som lärs ut i skolan idag kallas kort division, tidigare lärde man ut den långa divisionen som trappan och liggande stolen. De långa divisionerna används än idag och kan introduceras som alternativ. Kort division är effektiv när nämnaren består av ensiffriga tal, vid flersiffriga tal är denna metod inte längre den mest effektiva.
Det finns flera saker som kan göra att barn får problem med division. Det kan vara bristande tabellkunskaper, men det kan också vara bristande förståelse för hela begreppet division. En annan sak kan vara avsaknaden av alternativa beräkningsstrategier och metoder. Bristen metoder kan leda till att man inte kan hantera och göra skriftliga beräkningar med tvåsiffriga tal. Därför är det viktigt att skolan lär ut fler alternativ av beräkningsmetoder samt använder och lär ut hur man räknar division med miniräknaren.
Läs flera av våra artiklar om matte.
Och hur var det med prioriteringsordningen för räkneoperationer, igen? Hitta svaret här.
Copyright Zcooly AB 2025
