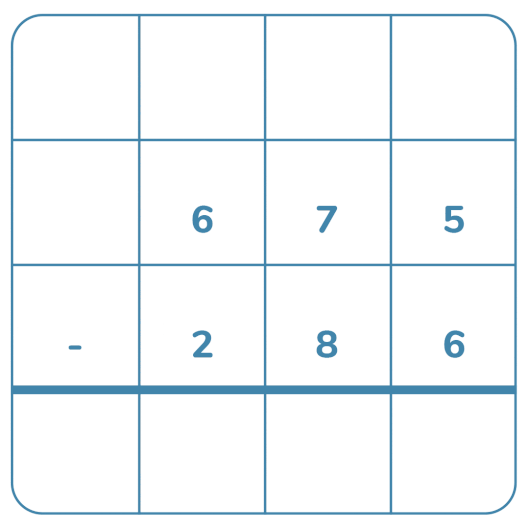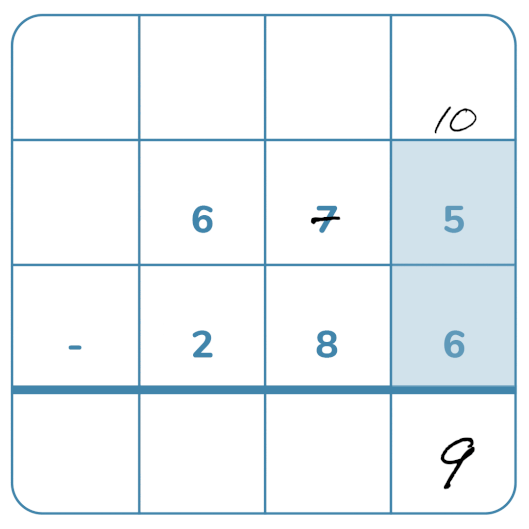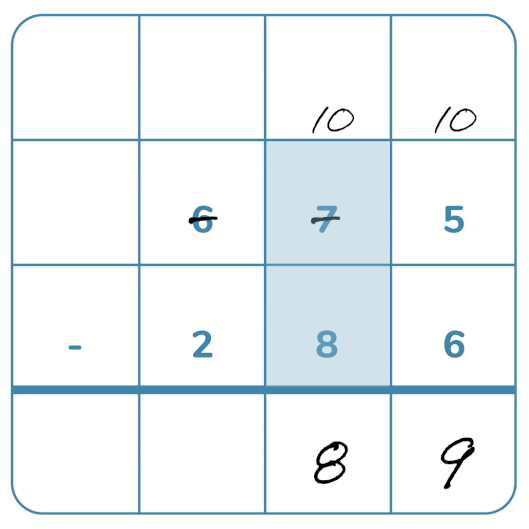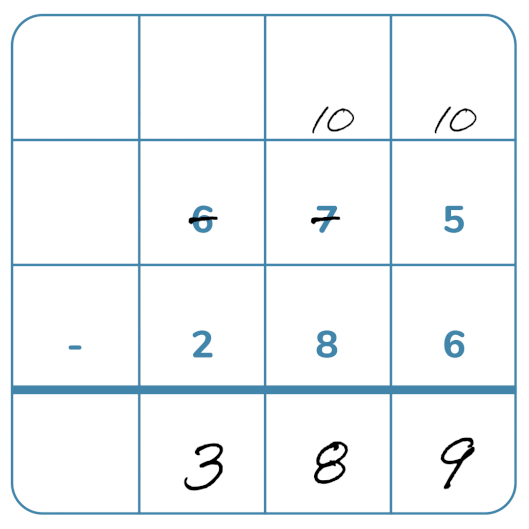
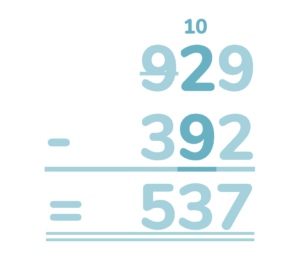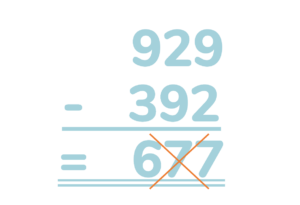Subtraktion med uppställning
Addition och subtraktion är de första räknesätten man lär sig. Till en början använder barn gärna konkret material för att förstå och räkna ut olika tal, för att sedan gå över och lära sig huvudräkning och andra olika strategier. När subtraktion introduceras är det bra att lära dem se sambanden mellan addition och subtraktion. Exempelvis kan man sina tiokompisar och vet att 2+8=10 vill vi att de då ska se sambandet 10-8=2 och att dubblorna 6+6=12 för att se sambandet 12-6=6. Då blir det lättare att förstå subtraktion med uppställning.
När barn ska avancera och starta med skriftliga beräkningar är det viktigt att de har en god taluppfattning, detta för att inte skapa förvirring. De behöver också förstå positionssystemet, decimalform och de behöver även ha automatiserade tabellkunskaper.